Which Sorting Algorithm Continuously Divides an Array Into Halves Until Single Elements Are Reached
In this article, we we talk about the merge sort algorithm. We will see some visual examples to help understand the algorithm and then implement it using Java and Python code.
What Is a Merge Sort Algorithm?
A merge sort algorithm is an efficient sorting algorithm based on the divide and conquer algorithm. It divides a collection (array) of elements into single units and then merges them in an orderly fashion.
Let's see an example to understand how merge sort works.
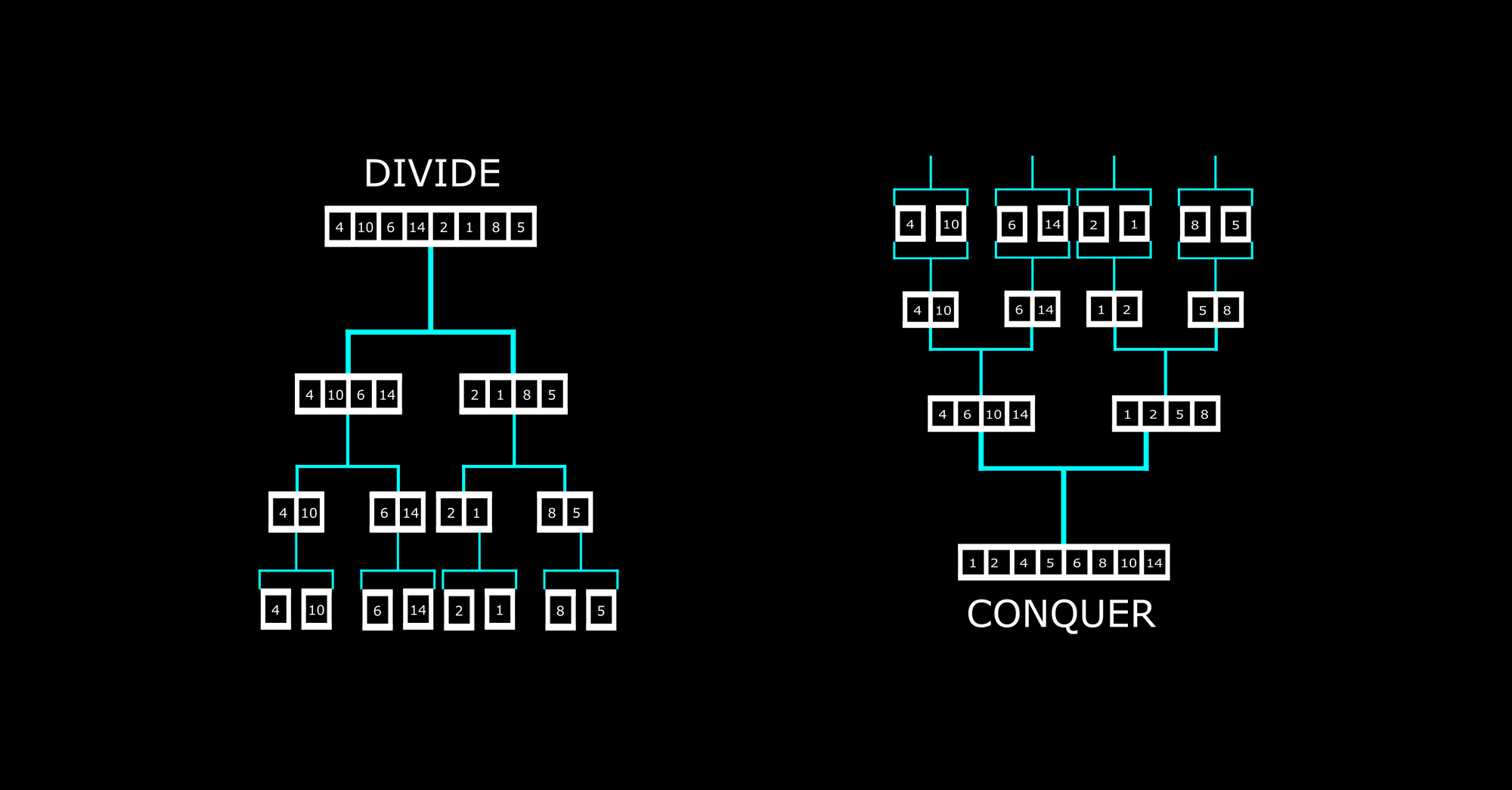
We are going to use the merge sort algorithm to sort this array of numbers: 4, 10, 6, 14, 2, 1, 8, 5
Here is an image to show you the "divide" process:
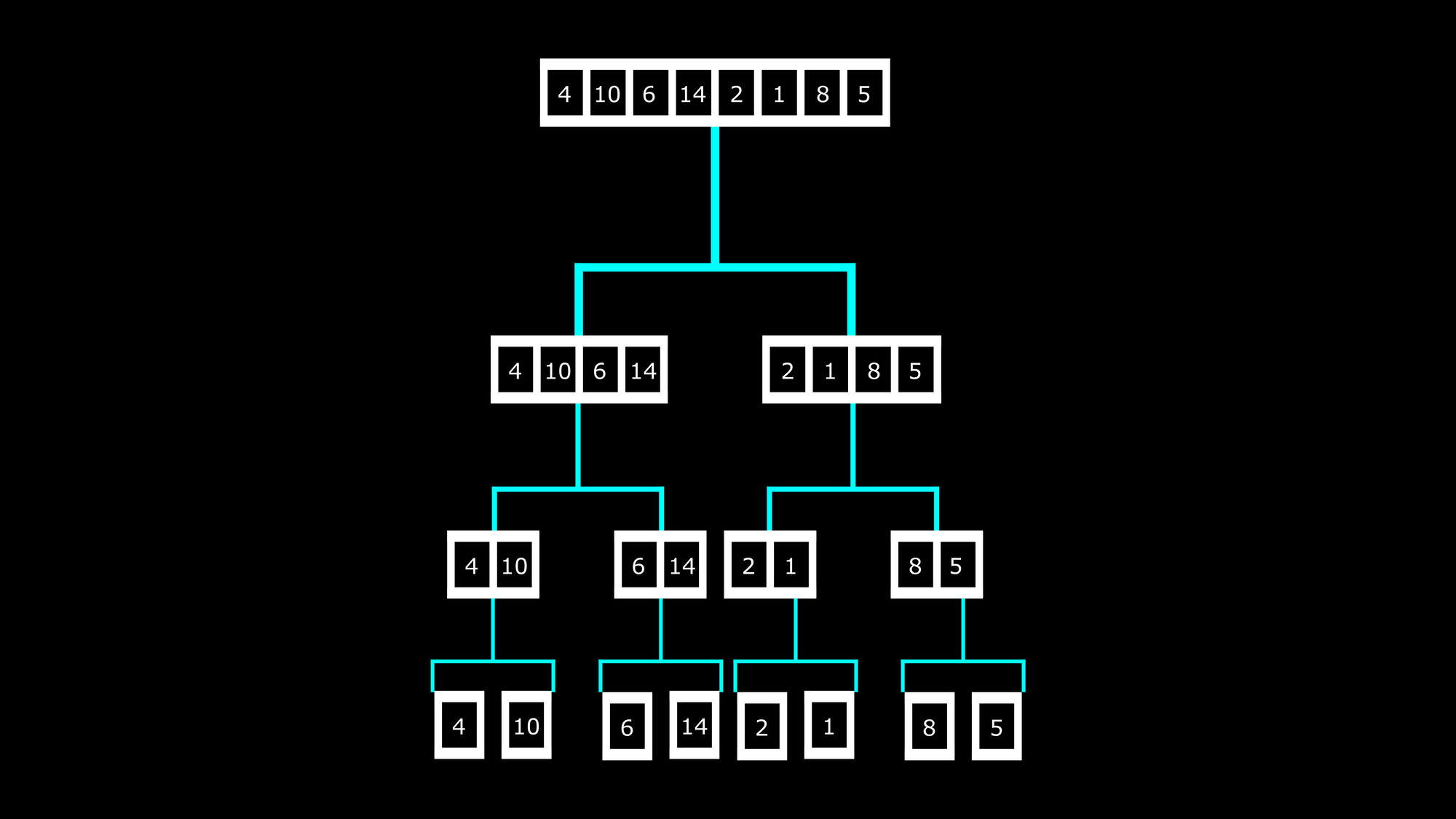
The array was first divided into two separate arrays. Then those arrays were also divided. This division continued until all the elements in the array became a single unit.
After this stage, merging starts. Here is how that happens:
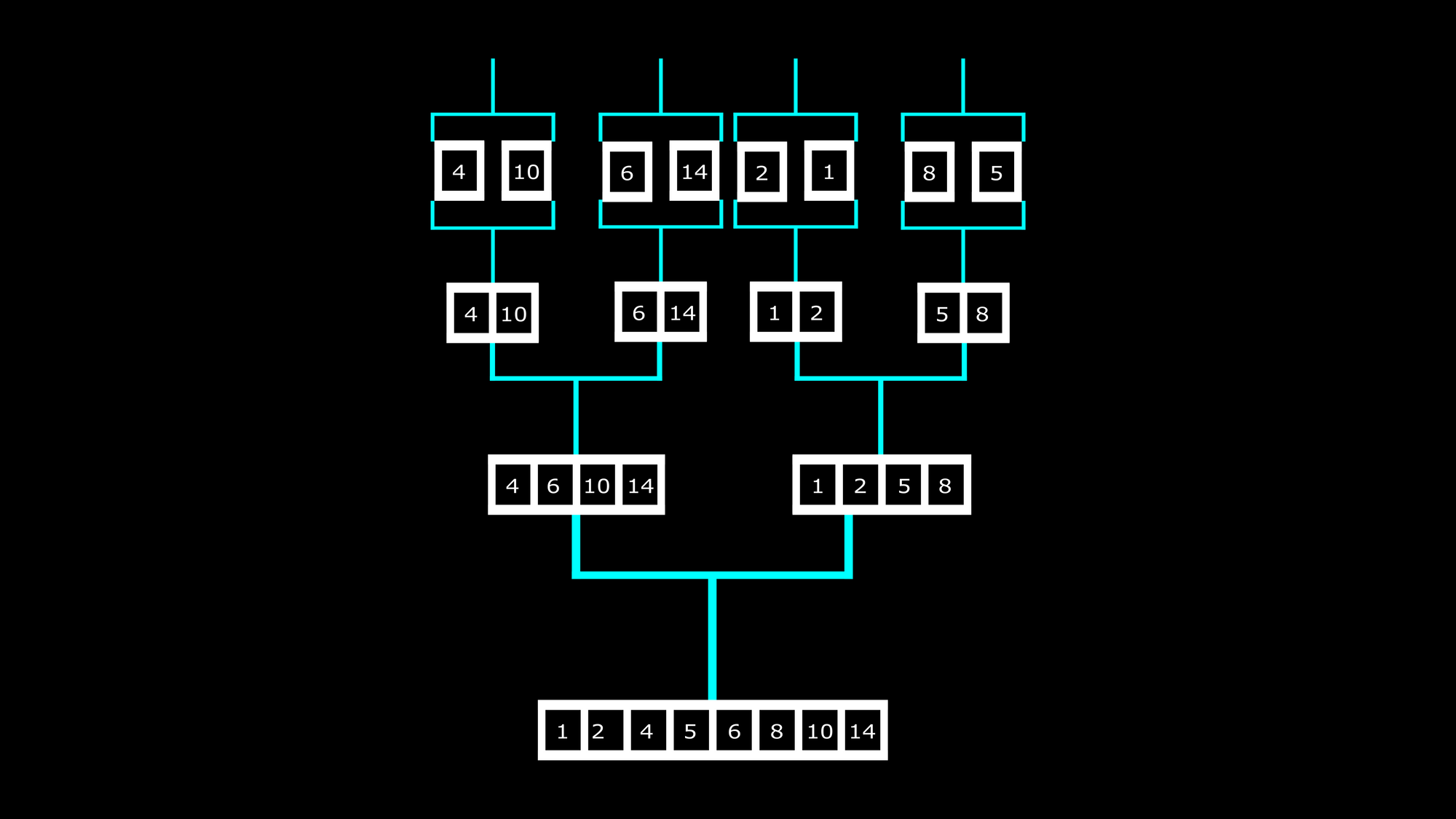
The elements are being regrouped into arrays but this time in a sorted order. In the same way they were split, they are being merged.
Before we implement this algorithm using code, you should understand how we are able to collect these elements in a sorted order.
We will use the section where we have regrouped the elements into two separate arrays – 4, 6, 10, 14 and 1, 2, 5, 8. Here is an illustration to understand how we arrived at the final array:
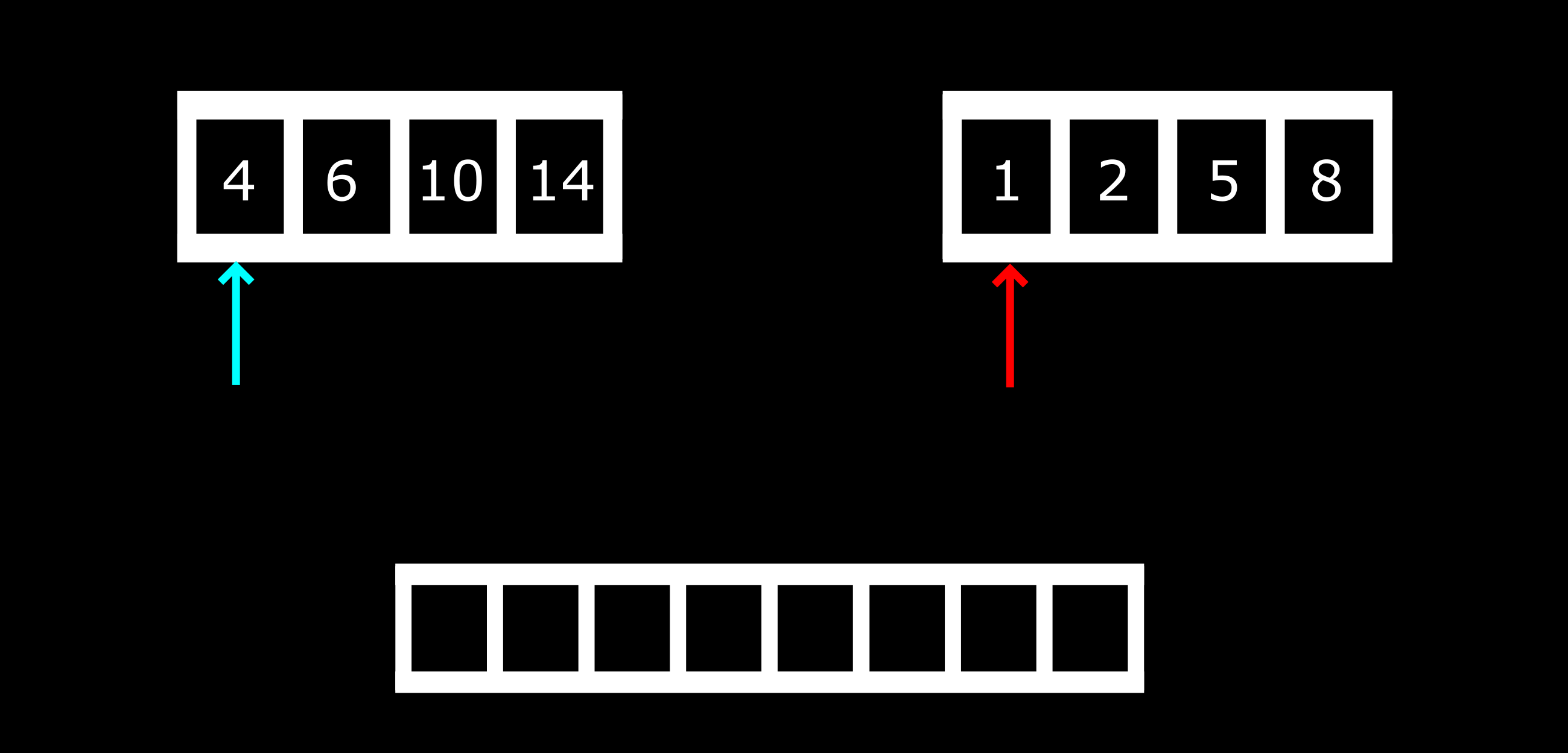
As can be seen above, we have two arrows pointing to the first index of both arrays. A comparison will be made to figure out which index is smaller. In our case, 1 is smaller than 4 so will be pushed to the merged array. Then the red arrow will move to the next index. That is:
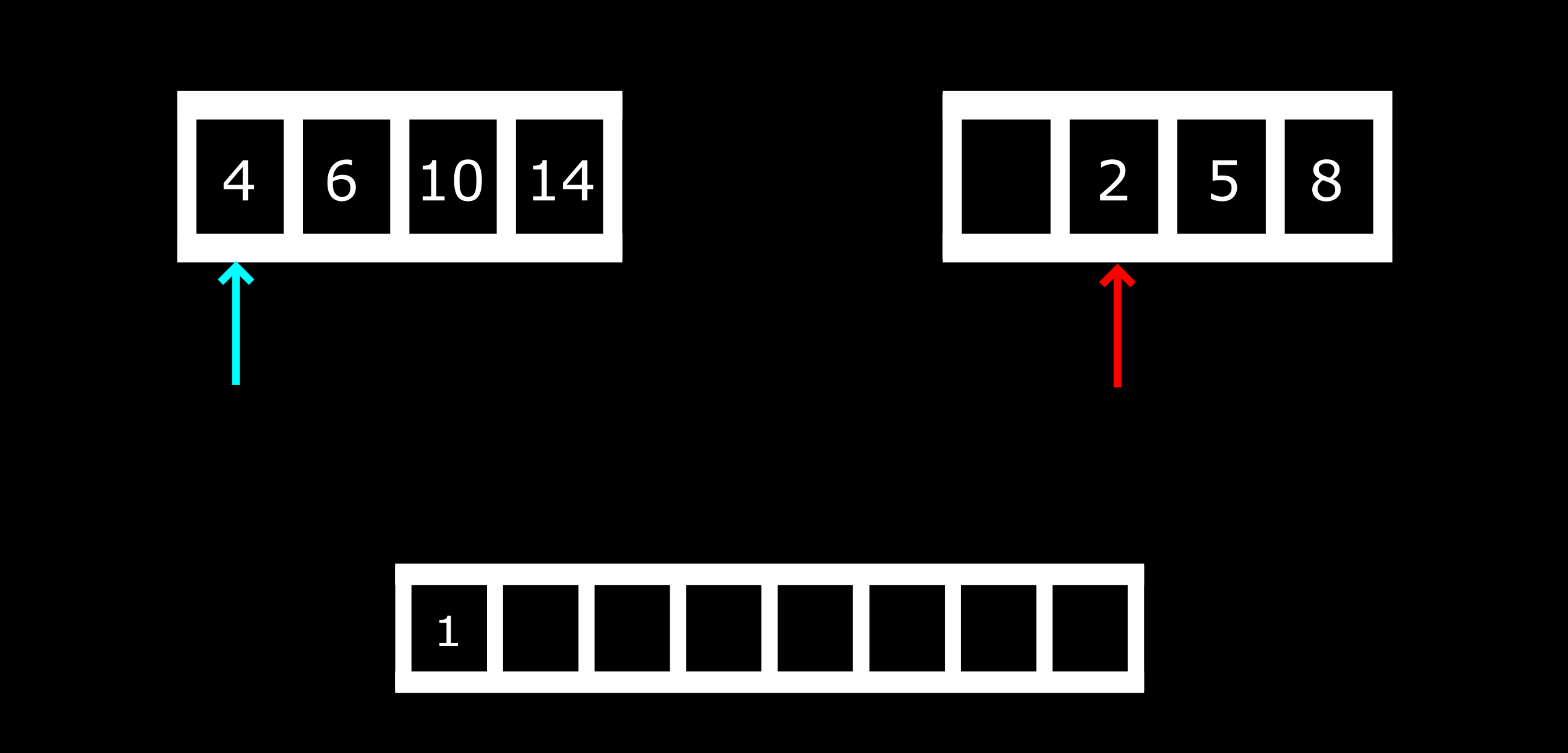
Another comparison will be made: is 2 < 4?
2 is less than 4, so it will be pushed to the merged array and the arrow moves to the next index.
For the next comparison:

4 is less than 5, so 4 will be pushed to the merged array and the cyan arrow will move to the next index.
This comparison will continue until the merged array gets filled up. If it gets to a point where one array becomes empty, the array with elements left will be copied into the merged array in a sorted order.
Let's see some code examples!
Merge Sort Example in Java
If we want to implement merge sort with Java, here's what that would look like:
public class MergeSort { public static void main(String[] args) { int[] numbers = {4, 10, 6, 14, 2, 1, 8, 5}; mergeSort(numbers); System.out.println("Sorted array:"); for (int i = 0; i < numbers.length; i++) { System.out.println(numbers[i]); } } private static void mergeSort(int[] inputArray) { int arrayLength = inputArray.length; if (arrayLength < 2) { return; } int midPoint = arrayLength / 2; int[] leftArray = new int[midPoint]; int[] rightArray = new int[arrayLength - midPoint]; for (int i = 0; i < midPoint; i++) { leftArray[i] = inputArray[i]; } for (int i = midPoint; i < arrayLength; i++) { rightArray[i - midPoint] = inputArray[i]; } mergeSort(leftArray); mergeSort(rightArray); merge(inputArray, leftArray, rightArray); } private static void merge (int[] inputArray, int[] leftArray, int[] rightArray) { int leftArrayLength = leftArray.length; int rightArrayLength = rightArray.length; int x = 0; int y = 0; int z = 0; while (x < leftArrayLength && y < rightArrayLength) { if (leftArray[x] <= rightArray[y]) { inputArray[z] = leftArray[x]; x++; } else { inputArray[z] = rightArray[y]; y++; } z++; } while (x < leftArrayLength) { inputArray[z] = leftArray[x]; x++; z++; } while (y < rightArrayLength) { inputArray[z] = rightArray[y]; y++; z++; } } } Let's break the code down.
public static void main(String[] args) { int[] numbers = {4, 10, 6, 14, 2, 1, 8, 5}; // 1, 2, 4, 5, 6, 8, 10, 14 mergeSort(numbers); System.out.println("Sorted array:"); for (int i = 0; i < numbers.length; i++) { System.out.println(numbers[i]); } } Above, we created our array of numbers. After that, we called the mergeSort method to sort the numbers. Then we looped through the array of sorted numbers and printed them to the console.
private static void mergeSort(int[] inputArray) { int arrayLength = inputArray.length; if (arrayLength < 2) { return; } int midPoint = arrayLength / 2; int[] leftArray = new int[midPoint]; int[] rightArray = new int[arrayLength - midPoint]; for (int i = 0; i < midPoint; i++) { leftArray[i] = inputArray[i]; } for (int i = midPoint; i < arrayLength; i++) { rightArray[i - midPoint] = inputArray[i]; } mergeSort(leftArray); mergeSort(rightArray); merge(inputArray, leftArray, rightArray); } We got the midpoint of the array by dividing the array length by two. The left array starts from the first index to the midpoint while the right array starts from the index after the midpoint to where the array ends.
We then created two loops to copy elements into the left and right array depending on the position of the elements. We then called the mergeSort method on the left and right array. This will keep breaking the array down recursively until the arrays have been reduced to single units (just like we saw in the images in the last section).
Lastly, we called the merge method to merge the arrays into one array in a sorted order. Let's have a look at the logic used in the merge method.
private static void merge (int[] inputArray, int[] leftArray, int[] rightArray) { int leftArrayLength = leftArray.length; int rightArrayLength = rightArray.length; int x = 0; int y = 0; int z = 0; while (x < leftArrayLength && y < rightArrayLength) { if (leftArray[x] <= rightArray[y]) { inputArray[z] = leftArray[x]; x++; } else { inputArray[z] = rightArray[y]; y++; } z++; } while (x < leftArrayLength) { inputArray[z] = leftArray[x]; x++; z++; } while (y < rightArrayLength) { inputArray[z] = rightArray[y]; y++; z++; } } Remember the arrows from the images in the last section? We have denoted them here using x and y then z for the merged array where the numbers will be pushed into in a sorted order.
The while loops were used to make the comparison on both arrays and change the position of x, y and z as the elements got pushed into the merged array.
Insertion Sort Example in Python
def mergeSort(array): if len(array) > 1: midPoint = len(array)//2 leftArray = array[:midPoint] rightArray = array[midPoint:] mergeSort(leftArray) mergeSort(rightArray) x = 0 y = 0 z = 0 while x < len(leftArray) and y < len(rightArray): if leftArray[x] < rightArray[y]: array[z] = leftArray[x] x += 1 else: array[z] = rightArray[y] y += 1 z += 1 while x < len(leftArray): array[z] = leftArray[x] x += 1 z += 1 while y < len(rightArray): array[z] = rightArray[y] y += 1 z += 1 def printSortedArray(array): for i in range(len(array)): print(array[i], end=" ") print() if __name__ == '__main__': numbers = [4, 10, 6, 14, 2, 1, 8, 5] mergeSort(numbers) print("Sorted array: ") printSortedArray(numbers) The logic here is exactly the same as in the last section. Above, we implemented the merge sort algorithm using Python. You can find an explanation of how the code works in the last section.
The time complexity of merge sort is O(n*Log n) for all cases (best, average and worst).
Conclusion
In this article, we saw learned how the merge sort algorithm works. We then saw some examples and how to apply it in our Java and Python code.
Happy coding!
Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started
kirkpatrickprimses.blogspot.com
Source: https://www.freecodecamp.org/news/merge-sort-algorithm-python-and-java-examples-with-time-complexity/
0 Response to "Which Sorting Algorithm Continuously Divides an Array Into Halves Until Single Elements Are Reached"
Post a Comment